Algorithm_2

Convex Hulls (Gift Wrapping Algorithm)

The convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it.
The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset.
For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. (Wikipedia)

leftmost_point = min(points)
convex_points.append(leftmost_point)
current_idx = points.index(leftmost_point)

leftmost_point_idx = current_idx
while True:
    next_point_2 = (leftmost_point_idx + 1) % len(points)
    for next_point_1 in range(len(points)):
        if next_point_1 != leftmost_point_idx:
            direction = self.cross_product(points[leftmost_point_idx], points[next_point_1], points[next_point_2])
            if direction > 0:
                next_point_2 = next_point_1
    leftmost_point_idx = next_point_2
    if leftmost_point_idx == current_idx:
        break
    convex_points.append(points[next_point_2])
convex_points.append(leftmost_point)

Example

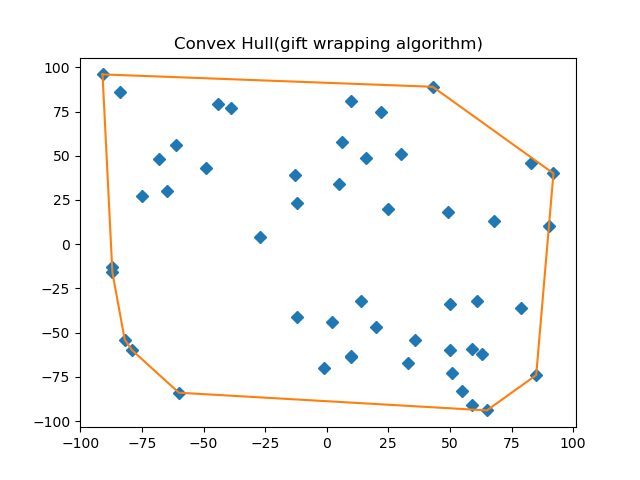
cross product : https://www.youtube.com/watch?v=eu6i7WJeinw

Convex Hull (Monotone Chain Algorithm / collinear)

points.sort()
upper = []
for p in points:
    while len(upper) >= 2 and cross(upper[-2], upper[-1], p) > 0:
        upper.pop()
    upper.append(p)

lower = []
for p in reversed(points):
    while len(lower) >= 2 and cross(lower[-2], lower[-1], p) > 0:
        lower.pop()
    lower.append(p)

return list(map(list, set(map(tuple, lower[:-1] + upper[:-1]))))