Algorithm from leetcode(2)

Partition Equal Subset Sum(leetcode-416)

Given a non-empty array containing only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.

bottom-up

# with only one number, we can form a subset only when the required sum is
# equal to its value
for j in range(1, s + 1):
    dp[0][j] = nums[0] == j

# process all subsets for all sums
for i in range(1, numsLen):
    for j in range(1, s + 1):
        if dp[i - 1][j]:  # if we can get the sum 'j' without the number at index 'i'
            dp[i][j] = dp[i - 1][j]
        elif j >= nums[i]:  # else if we can find a subset to get the remaining sum
            dp[i][j] = dp[i - 1][j - nums[i]]

memoization+dfs

if remain in self.cache:
    return self.cache[remain]
if remain == 0:
    return True
if remain < 0 or i == len(self.nums):
    return False
self.cache[remain] = self.dfs(remain - self.nums[i], i + 1) or self.dfs(remain, i + 1)
return self.cache[remain]

Find First and Last Position of Element in Sorted Array(leetcode-34)

Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.

def search(nums, target):
    n = len(nums)
    position = n
    left,right = 0, n-1
    while left <= right:
        mid = (left+right) // 2
        if nums[mid] >= target:
            position = mid
            right = mid-1
        else:
            left = mid+1
    return position

It is a key to think first positions of target and target+1.

For example, suppose there are nums like 3 3 3 5 5 5 6 7 8 and target is 5.

First, find the first position of ‘5’ and then find the first position of ‘6’. first position of ‘6’ - 1 will be the last position of ‘5’.

Minimum Height Trees (leetcode-310)

while n > 2:
    n -= len(leaves)
    new_leaves = set()

    for leave in leaves:
        neighbor = graph[leave].pop()
        graph[neighbor].remove(leave)
        if len(graph[neighbor]) == 1:
            new_leaves.add(neighbor)

It is a key to remove every leaves from the graph until 2 nodes left.

Best Time To Buy and Sell Stock (leetcode-121)

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

for n in prices:
    if n < min_:
        min_ = n
    else:
        max_ = max(max_,n-min_)

Split Array Largest Sum (leetcode-410)

Given an array nums which consists of non-negative integers and an integer m, you can split the array into m non-empty continuous subarrays.

def cnt_p(value):
    cnt, cur = 0, nums[0]
    for i in range(1,len(nums)):
        if cur + nums[i] > value:
            cur = nums[i]
            cnt += 1
        else:
            cur += nums[i]
    return cnt

It is a key to use Binary Search. The search range will be from maximum of the nums’s array to sum of the nums’s array.

Longest Mountain in Array

Given an array A of integers, return the length of the longest mountain.

left, right

n = len(A)
a = [0]*n
b = [0]*n

for i in range(n-1):
    if A[i] < A[i+1]:
        a[i+1] = a[i]+1


for i in range(n-1,0,-1):
    if A[i] < A[i-1]:
        b[i-1] = b[i]+1

ans = 0

for i in range(n):
    if a[i] != 0 and b[i] != 0:
        ans = max(ans,a[i]+b[i])

return ans+1

###

n = len(A)
up,down,ans = 0,0,0

for i in range(1,n):
    if A[i-1] == A[i] or (down > 0 and A[i-1] < A[i]):
        up = down = 0
    if A[i-1] < A[i]:
        up += 1
    if A[i-1] > A[i]:
        down += 1
    if up and down:
        ans = max(ans, up + down + 1)

return ans

###

n = len(A)
l,r,ans = 0,0,0

for i in range(1,n-1):
    if A[i-1] < A[i] > A[i+1]:
        l = r = i
        while l > 0 and A[l-1] < A[l]:
            l -= 1
        while r < n-1 and A[r+1] < A[r]:
            r += 1
        ans = max(ans, r-l+1)

return ans

Pseudo-Palindromic Paths in a Binary Tree (leetcode-1457)

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

def dfs(node, seen):
    nonlocal ans

    seen ^= (1 << node.val)

    if node.left:
        dfs(node.left, seen)
    if node.right:
        dfs(node.right, seen)

    if not node.left and not node.right:
        if seen & (seen-1) == 0:
            ans += 1

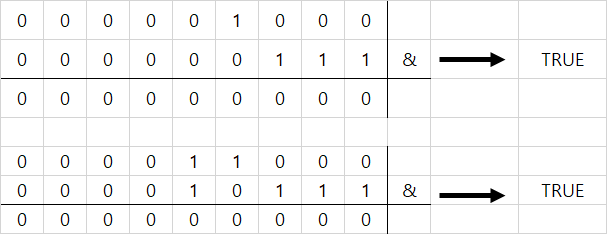
It is a key to use bitmask in order to use less space complexity.